
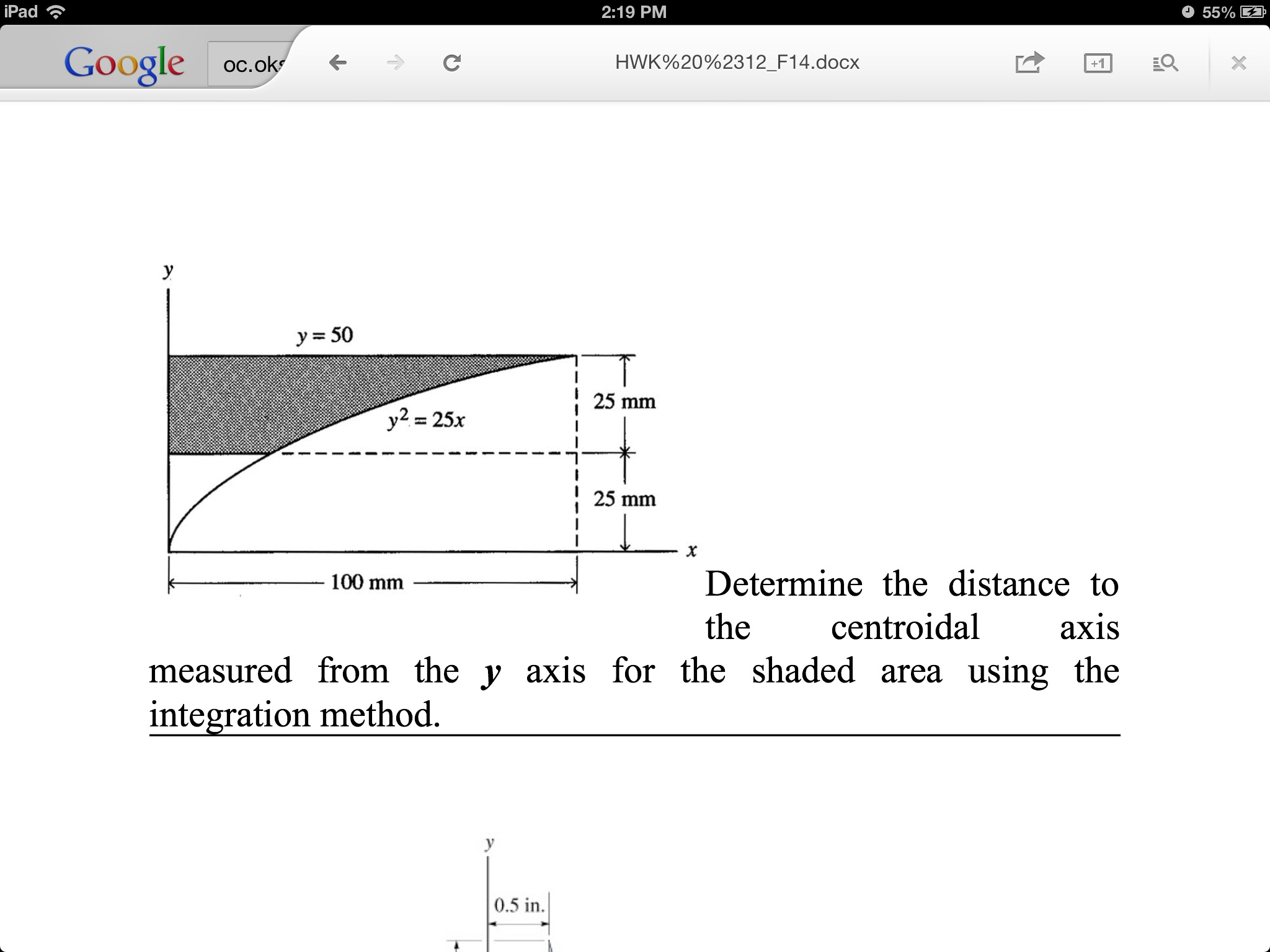
The improved locations show that the northern Endeavour segment ruptured southwards from 48.3°N to 48.05°N during two diking events in early 2005, possibly accompanied by diking on the West Valley (WV) propagator. Despite the small footprints of networks near the segment center, locations show good agreement with geologic features at segment ends. The catalog comprises >85,000 earthquakes located using three-dimensional segment-scale P and S wave velocity models from a prior tomography experiment. We present >50,000 new earthquake locations for 2016–2021 from the Ocean Networks Canada NEPTUNE cabled observatory and relocate earthquakes from two autonomous networks in 19–2006. I need to know the y-bar of half of a sector in order to multiply that number by its area and compare it with the rest of the weights of the other elements.We use ocean bottom seismometer data from the Endeavour segment of the Juan de Fuca ridge to construct a long-term earthquake catalog for an intermediate spreading rate mid-ocean ridge.

There are two sectors in the problem, and they are both cut in half, which means they have an x and a y-bar as the centroid instead of just sitting in the middle of the axis. Here's a picture hopefully describing it better: This makes the y-bar for the sector centroid 0. The problem I have is the formula for a circular sector has the middle of the sector resting on the x-axis, with both angles (alpha) equally above and below the x-axis. But you need the y coordinate of this centroid. What does it mean? You denoted it with x-bar.
FIND XBAR AND YBAR OF THE SHADED AREA HOW TO
But you must use it if you do not know how to integrate.Ĭheck your formula for the centroid of the sector. This method you applied is very complicated. Have you learned simple ones? Because this double integral is an integral with respect to the angle (here comes in the cosine) then the result integrated with respect to the radius. Which is my final answer to this question. The overall Y-bar coordinate of the centroid of this figure is found by dividing the sum of the y-coordinate areas by the total area of the figure, or: Since the Areas of these figures are being subtracted from each other, their y-bar*Areas must too be subtracted: The y-coordinates of the elements multiplied by their respective areas are:įor the larger semi-circle: y-bar * A = (.5*pi*(r2)^2)*((4(r2))/(3*pi))įor the smaller semi-circle: y-bar * A = (.5*pi*(r1)^2)*((4(r1))/(3*pi)) Y-bar = sum of the y-bar centroids of each element multiplied by each individual area/total area

If the overall Y-bar or y-coordinate of the centroid of the figure is found by the equation: Where r1 is the radius of the smaller semi-circle and r2 is the radius of the larger semi-circle. The total area of the figure is given by the subtraction of the areas of all these figures, which is: Where alpha is 1/2 the angle of the sector. The formulas for the Area and centroid of the semi-sectors respectively are: The formulas for the Area and centroid of the semicircle The Y-bar because is zero and lies on the y-axis, and where r is the radius.
The formulas for the Area and centroid of the semi-circle respectively are: If I subtract the Area of the larger semi-circle and the smaller semi-circle, I get a half-donut, and if I subtract it further by the Area of the 2 partial sectors of a circle, I get the Area of the figure in question (less than half a donut). Separating this partial donut into other geometric figures yields: What the figure is is a little less than half a donut, depending on what alpha is. The work I've shown is tabulated which is why I chose not to write it out, but I'll do my best to explain it: Where the x is the distance from the y-axis to the element, and y is the distance from the x-axis to the element. The formula for the centroid via integrals is: Would you please type in your attempt of solution.Ī centroid is the center of gravity of a figure. What is the definition for the centroid? Have you learned the definition using integrals?


 0 kommentar(er)
0 kommentar(er)
